Hypergraphs and RDF

Hypergraphs and RDF (Resource Description Framework) are two distinct models used for representing and organizing data.

They have different applications in the field of computer science and knowledge representation, each offering unique approaches to structure and relate information.

A hypergraph is an extension of a graph where an edge can connect more than two nodes. In a hypergraph, an edge, known as a hyperedge, can link any number of vertices, offering a more flexible representation for complex relationships among data elements.

On the other hand, RDF is a standardized framework by the World Wide Web Consortium (W3C) for describing and exchanging information on the web. RDF uses a graph-based model to represent data, where nodes represent resources, and edges denote relationships between these resources.

While hypergraphs provide a generalized approach for modeling relationships, RDF is specifically designed for web-based data interchange. Both models play important roles in diverse applications, and understanding their characteristics is crucial for effective data representation and manipulation.

The topic of hypergraphs has come up of late in a couple of different discussion groups, and it seems like a good opportunity to explore what they are, and how they fit (or don’t) in the broader RDF ecosystem.

Evolving to Hypergraphs

In an ordinary graph, you have nodes and edges, with each node connected to another node along an edge.

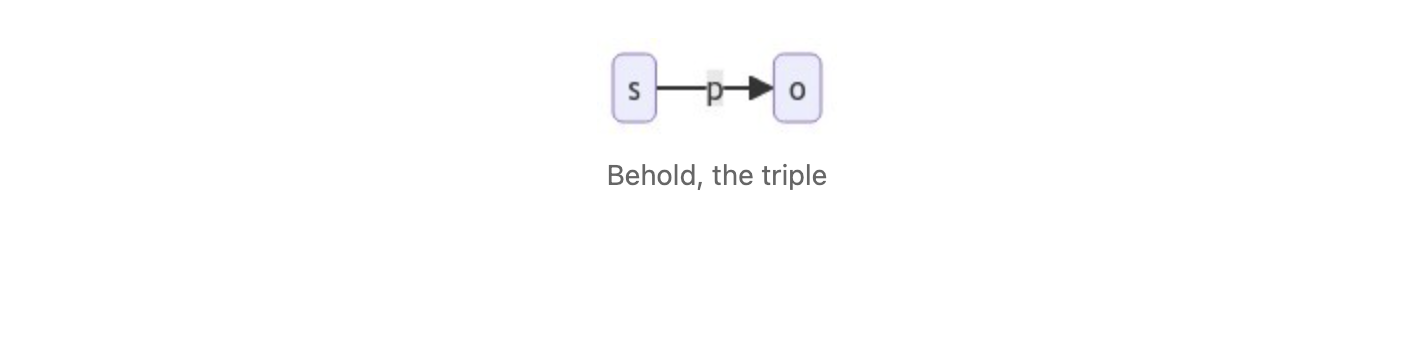
In Turtle, this is expressed in about as simple a manner as you can imagine:

where s represents a subject node, p a predicate edge, and o, an object node.

Let’s say that you have three triples where you have the same subject and predicate but different objects:

It is also possible to have multiple object nodes associated with the same subject and predicate:

However, it’s worth noting here that while RDF here treats them as separate assertions, Turtle does not.

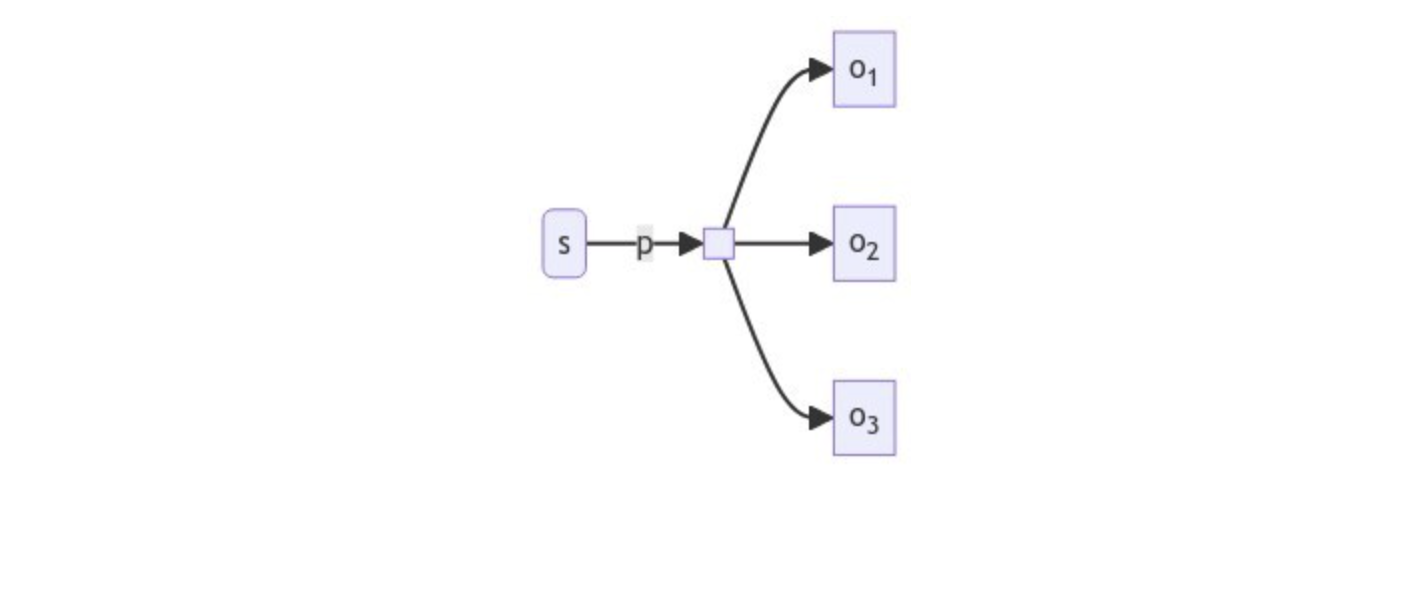
This is an interesting observation, because it suggests that Turtle is more than just a syntactical sugar - it seems to suggest that RDF has the ability to have a set of objects associated with a triple. At least in the direction from subject to object, Turtle is describing what’s known as a hypergraph.

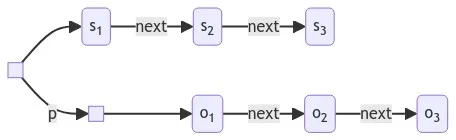
Loosely, a hypergraph can be thought of as a graph in which a single node can, through its edge, be associated with a set of nodes. In the case of Turtle, this expression is indicated through the simple sequence:

Now, I want you to focus on that small square in the middle of the diagram. This is the bridge that connects the world of Turtle (and hypergraphs) with the world of rdf. What this is actually saying is that there is construct that consists of a simple bag of nodes, and what is actually being pointed to is this construct. Put another way, the above statement could decompose as follows in Turtle:

So arguably, RDF isn’t really a hypergraph … it’s a trick! Well, perhaps.

A set is a thing, consisting of a collection of other things. In other words, if you look upon the blank node discussed here as an object, then what this notation actually says is that _:b1 is a set, whose members are o1, o2, and o3. This is pretty much the definition of a hypergraph.

Now, this covers the object direction, but the subject direction is not quite as forgiving. For instance, suppose that I wanted to have multiple subjects sharing the same object, as in:

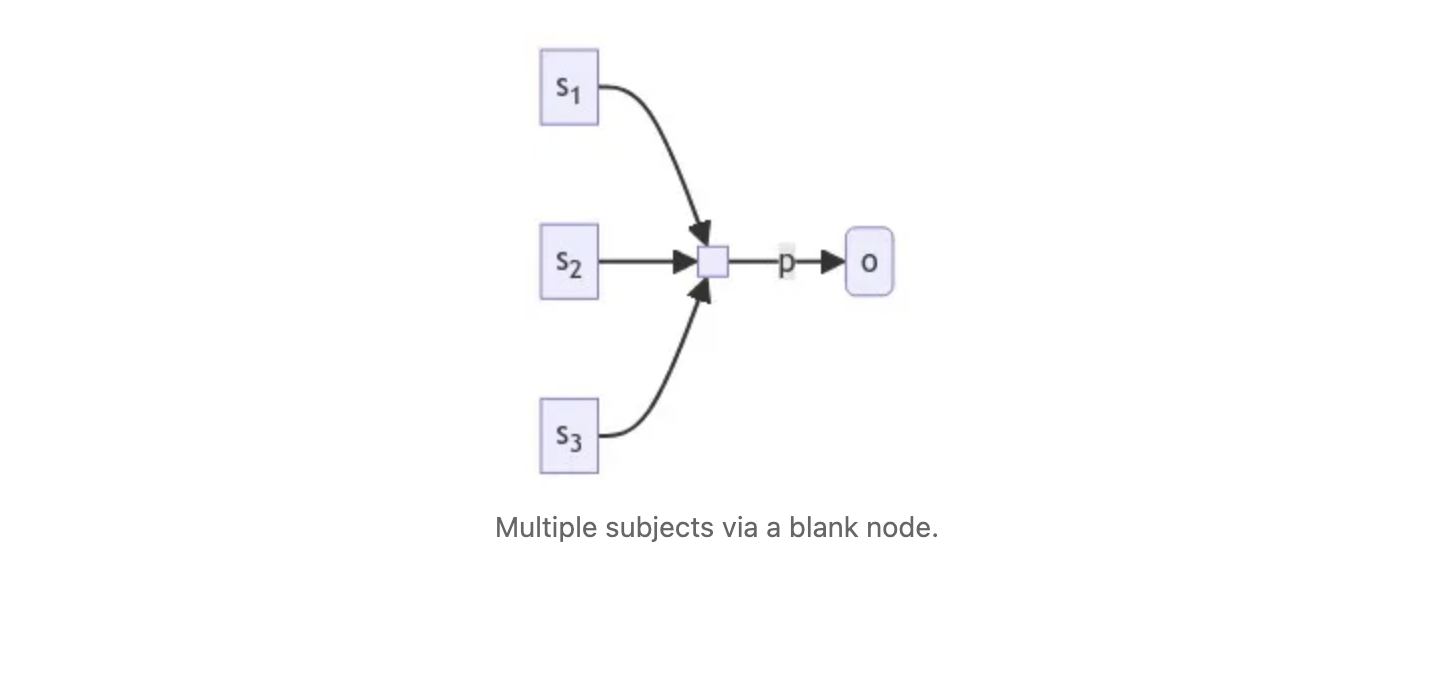
Once again, you are passing a set as an argument. The turtle here is roughly symmetric to the object case:

Now, it would be great if you could just say:

However, you can’t, primarily because this pattern wasn’t included in the Turtle parser (it likely breaks other things in Turtle as well). There are also no specialized markers for delineating a set in Turtle. Thus, at first glance, the idea of creating a true hypergraph goes out the window.

However, not all hope is lost. There is another structure within Turtle that can be delineated: the RDF List. RDF Lists are pretty ugly looking things:

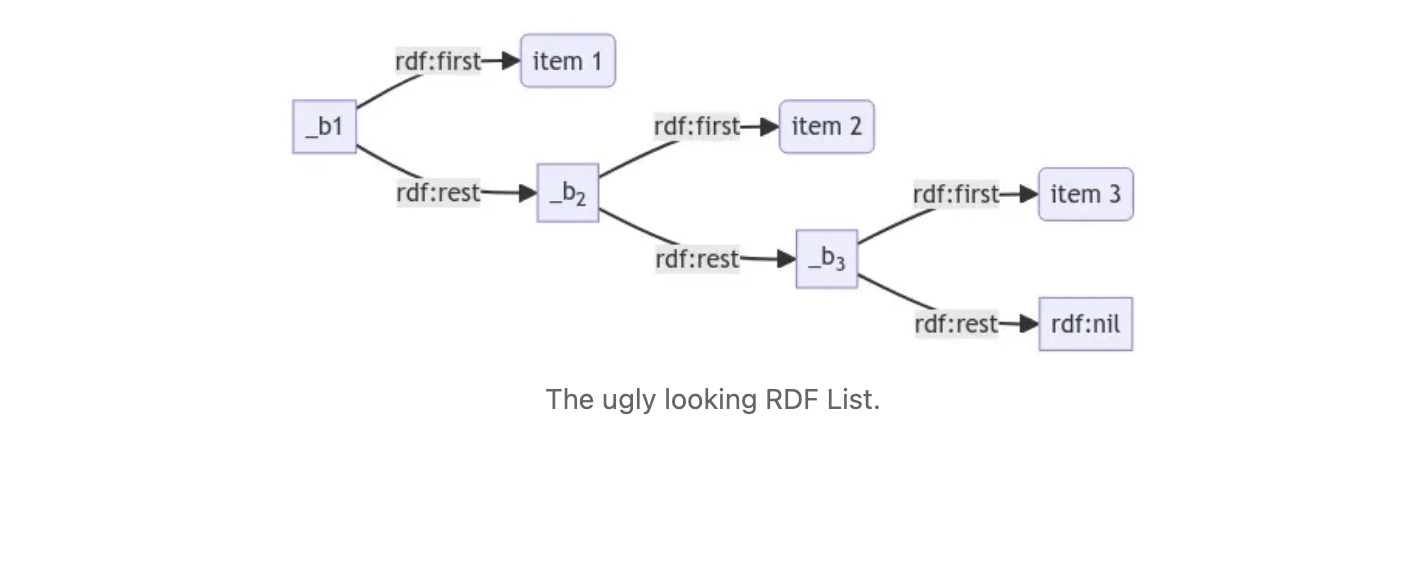
This is about the simplest implementation of a linked list that you can create in a graph. However, it’s complicated enough that Turtle does have a notation for it, of the form:

This notation has two advantages. First, it preserves the order of the list, something that a set doesn’t generally do. Additionally, the first blank node in the linked list (_:b1 here) serves as a pointer to the list. This means that by passing _:b1 you are passing what amounts to a list or array of items by reference.

This has very intriguing implications. Among other things, it means that you can pass such an array as the subject, meaning that once again Turtle is able to describe a hypergraph, this time on the subject node:

You could pass it on the object node in the same way, of course:

You could even do it with both:

This means that the “conceptual graph” that Turtle represents is a hypergraph, even if the underlying RDF implementation is not.

So what use is this? At it’s simplest, the fact that you can pass lists means that you can process lists in an explicit order. Let’s say you have the following Turtle code:

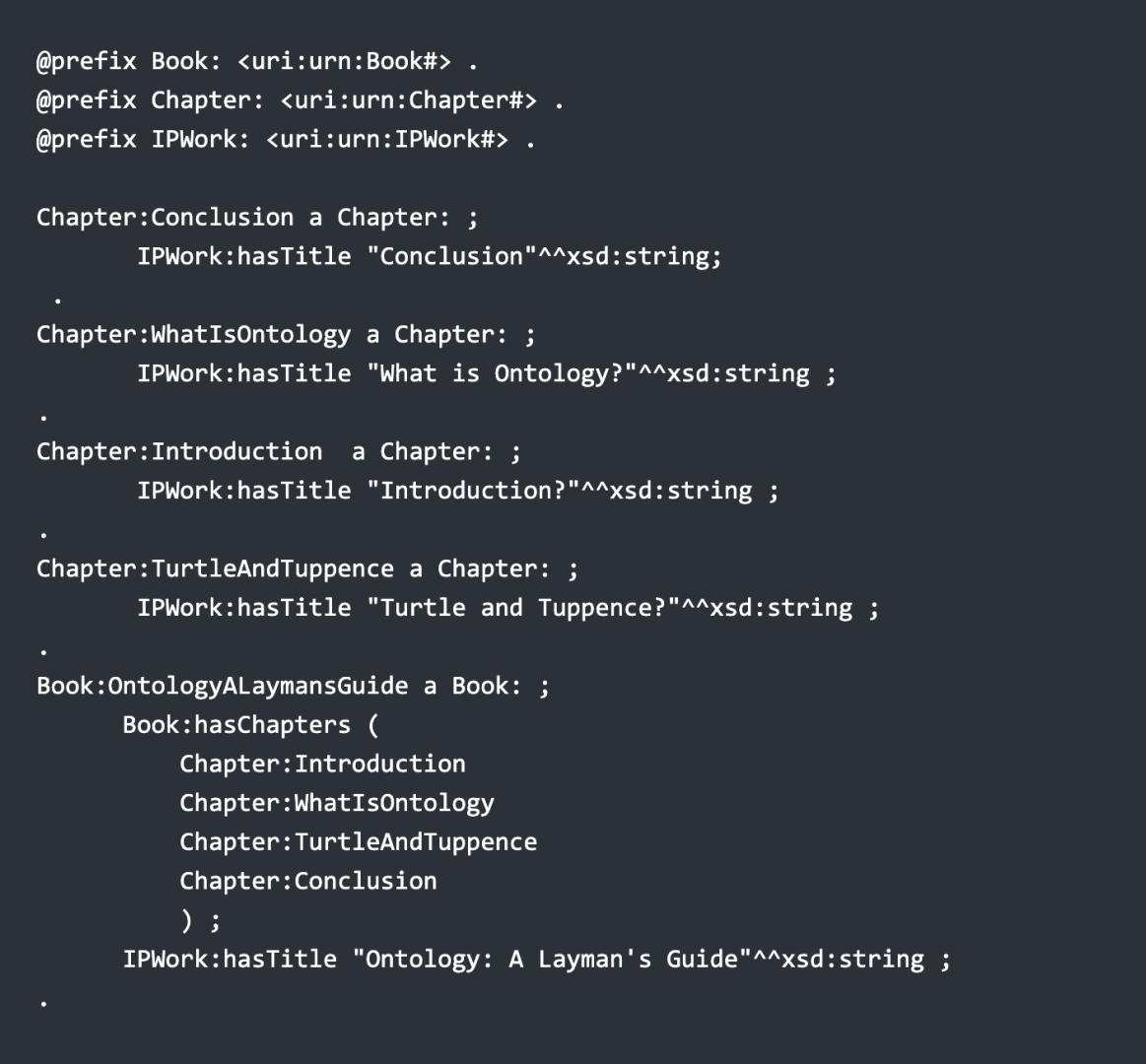
A SPARQL query can then use this information to create a listing of the chapters of the book in the correct order:

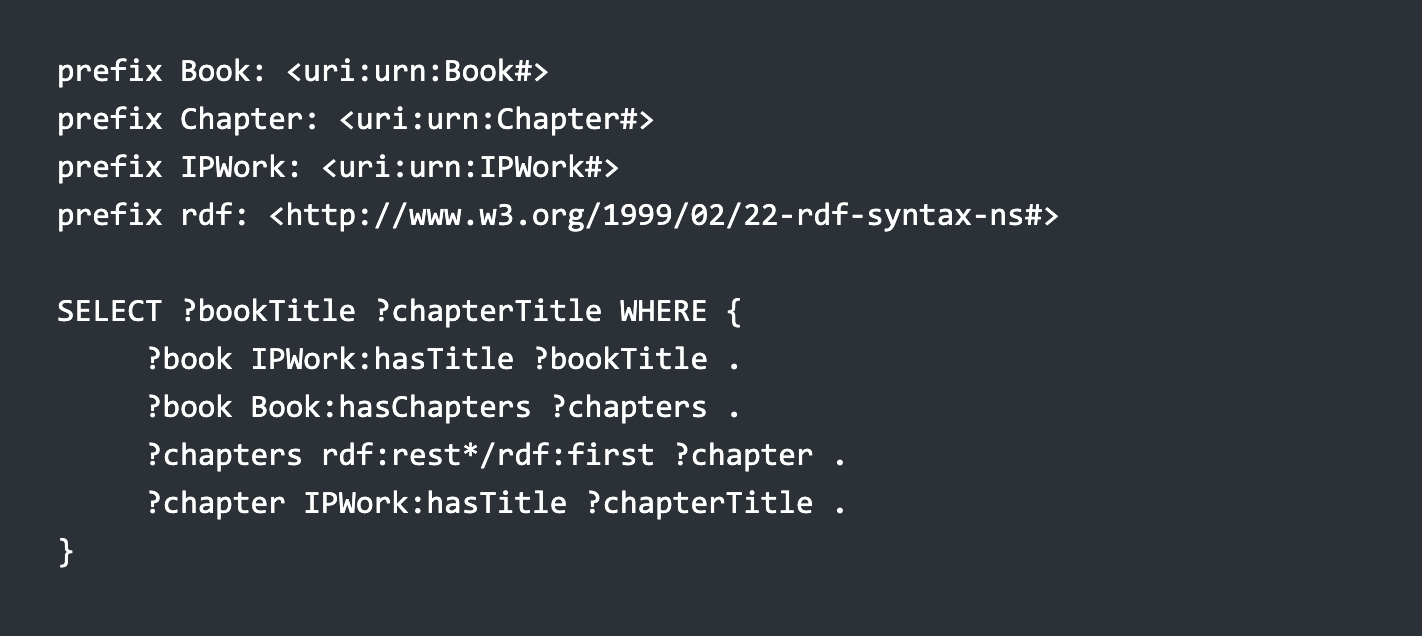
This will generate a table with the chapters in the specified order.

The expression illustrates walking a list, with the rdf:rest using transitive closure (walking along the same predicates in a path until the subject node no longer has the rdf:rest property), extracting for that node the relevant first item or ignoring it, if it’s reached rdf:nil.

The upshot of this is that while RDF by itself is not a hypergraph, the abstractions brought about with Turtle can make it a hypergraph easily enough.

Object Hypergraphs

In a relational database, a given table can have only one foreign key to another table per column. You can think of each foreign key per column as being an outbound link. for the concept embodied by the resource identified by the row.

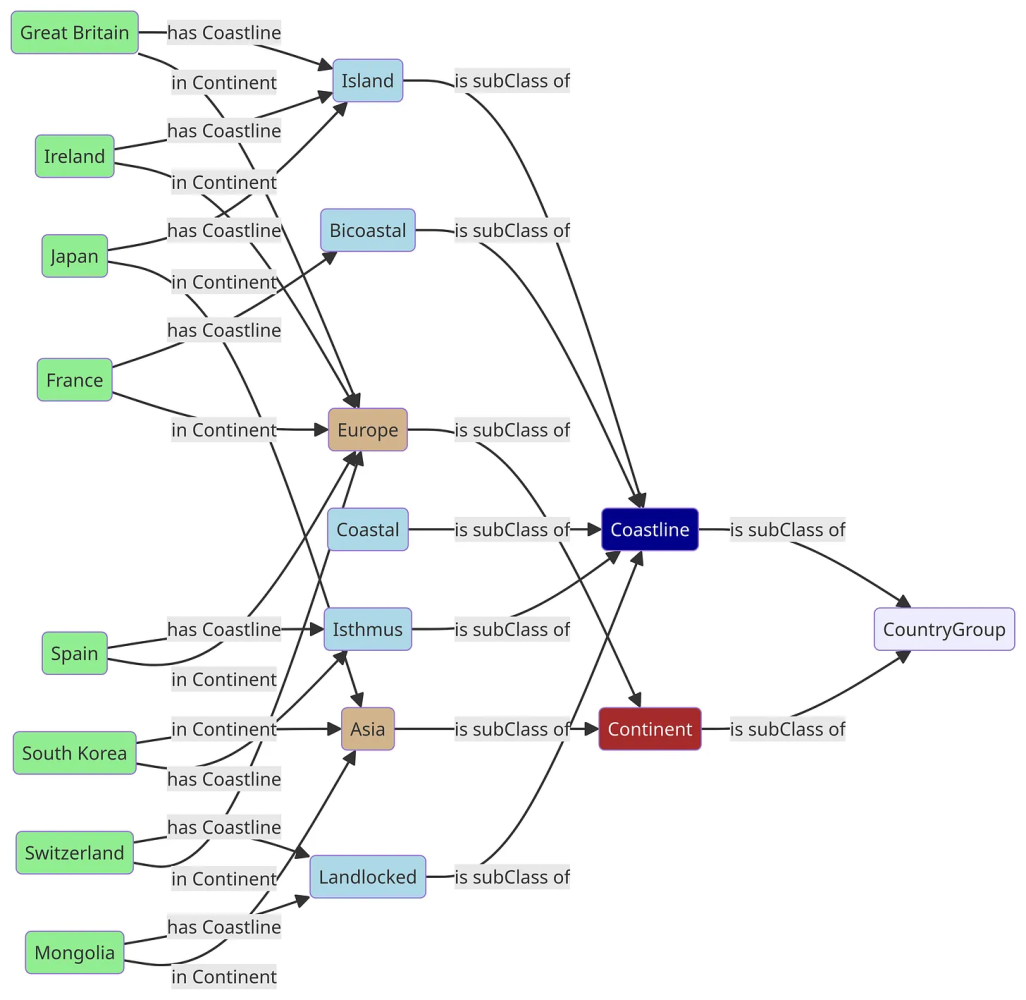
In one particular project I was involved in, countries could be qualified by country groups that described various characteristics of the countries. A simple example of this can be seen in the diagram below:

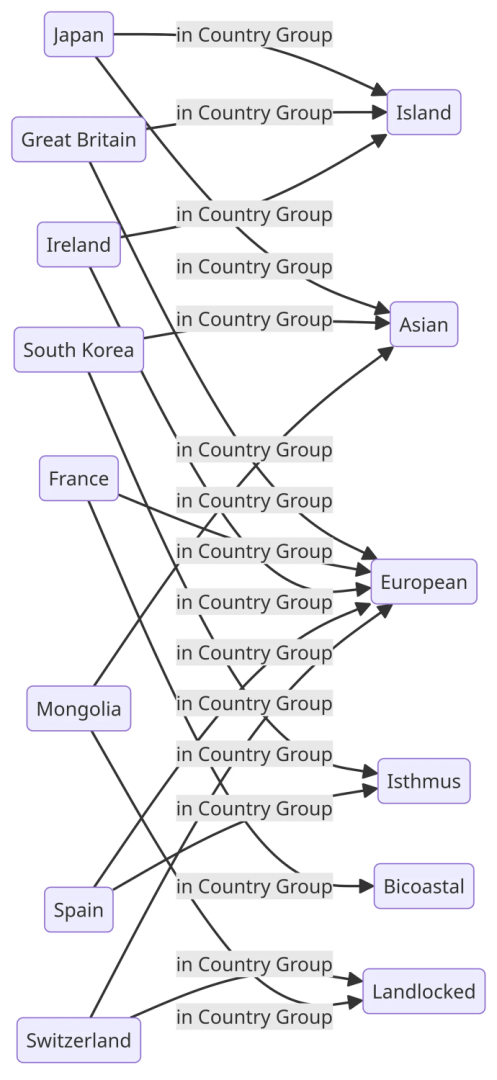
This corresponds to a Turtle file that looks (in part) something like this:

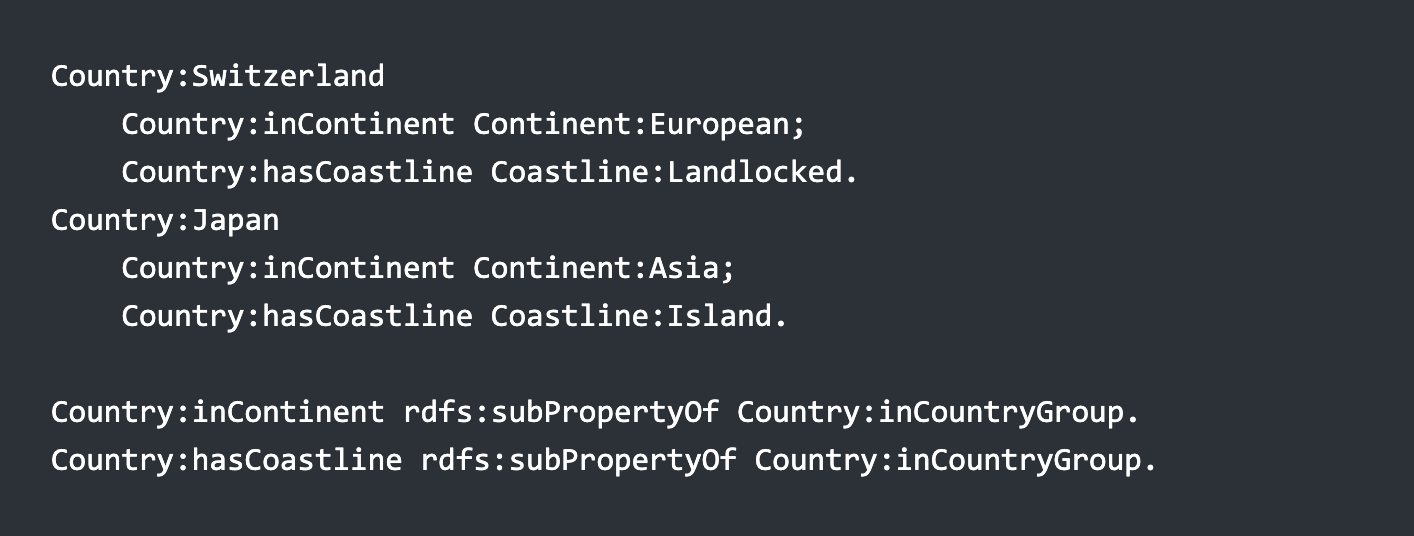
This is a hypergraph on the object side, because each country has more than one foreign key pointer. This is also a common design pattern where you have multiple tags that can be associated with a given concept. It should be noted, though, that if these tags are enumerations, such as the ones given above, there may, in fact, be some kind of underlying structure that is hidden in this model. For instance, the same information may also be stated as follows:

This, in turn, changes the Turtle, though only by normalizing two subclasses and creating two sub-properties:

Put another way, you can achieve many of the same effects that hypergraphs give you by combining good design and working with reference pointers, as the book and chapter’s example in the previous section illustrates. Once you understand this point, hypergraphs aren’t all that scary, though they can help you push the boundaries of what you’re attempting to model.

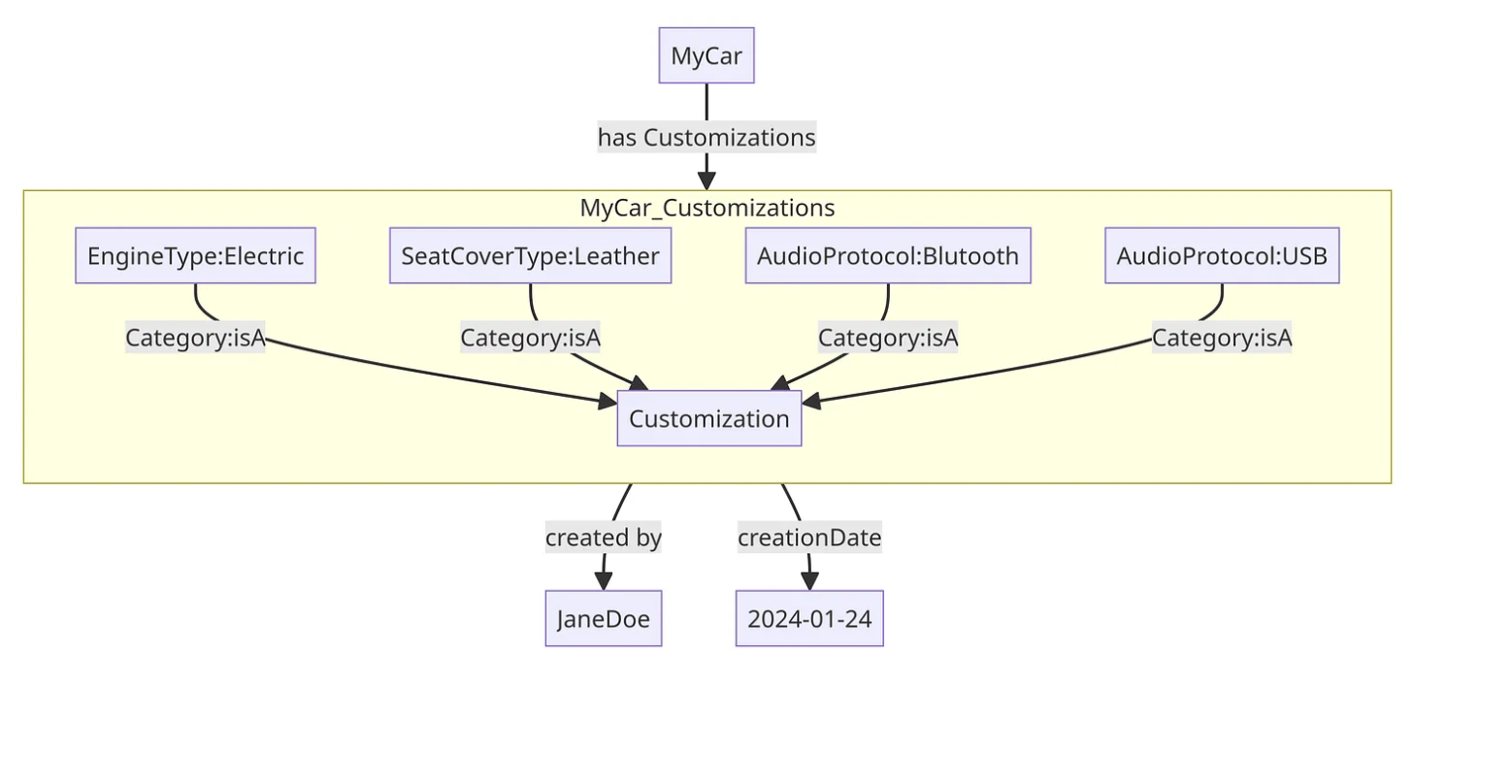
I encountered this particular problem once when attempting to build a model for relating cars being sold to custom features for that car. This list could be quite extensive, often with dozens of such features for a given car, and my first inclination - to simply create a single list of customizations, very quickly became unworkable from a UI standpoint (replace inCountryGroup above with hasCustomization, and you get an idea of what this looked like). However, by using cascading categories (engineType, seatCoverType, etc.), I replaced a single large block with a number of properties. By creating a pointer to a list of such properties, I could then put all the customizations on a separate page.

There are two different ways to model this, as shown below:

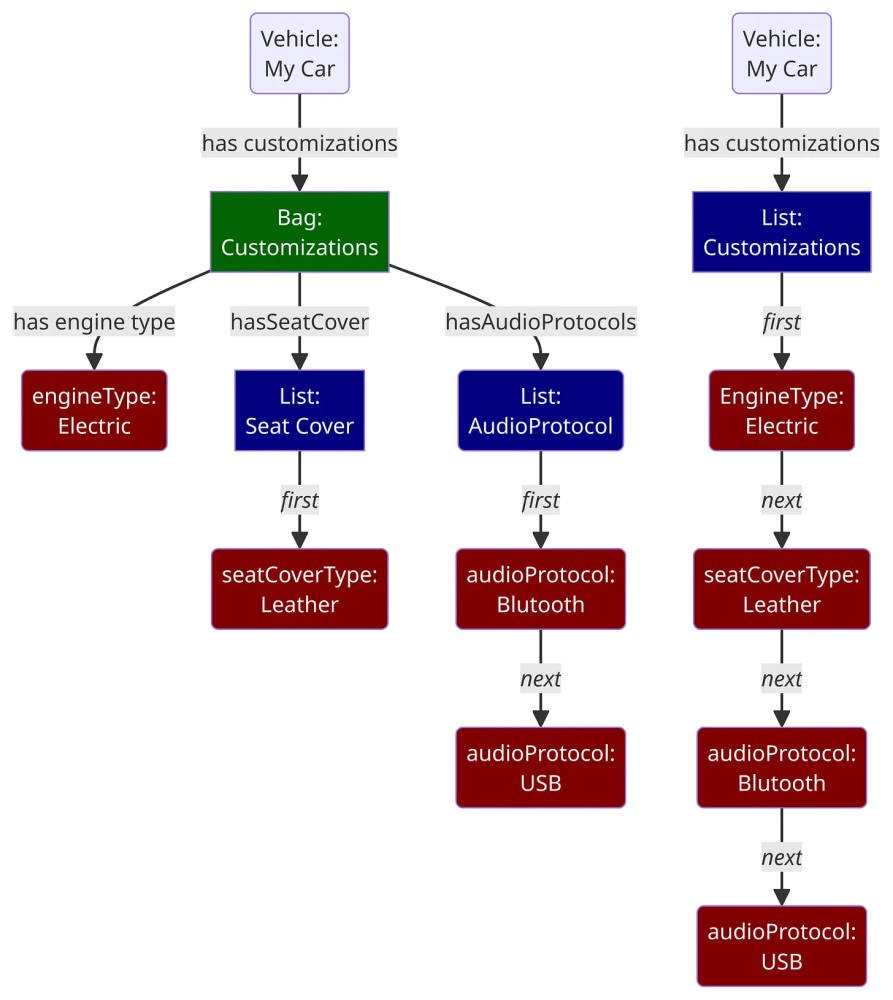
The bag approach is shown on the left and can be considered a bag (or set) of lists. In this case, the square-edged boxes represent blank nodes, while the rounded-edged boxes are IRI nodes. The list approach, on the right, is typically of a hypergraph, in which you have a list of (here, category) nodes without an attending structure. Which is preferable? My own experience has been the bag approach, largely because there is less in the way of computation needed to determine grouping structures.

You may also be questioning what happens when you have mutually exclusive options. The engine type is an example of this. You could have an electric car, an internal combustion engine (ICE), a rotary engine, a fuel cell, or a hybrid engine, but you usually don’t have more than one (I consider a hybrid to be a different engine type altogether, as it represents a distinct architecture even though it has aspects of both electric and ICE).

This is what makes lists so tricky. A list can be considered a pseudo-element, requiring a certain amount of additional processing and conditional logic when querying, but can be thought of as being of the same type as its constituent items. what changes is the shape of the connection? In SHACL, this would look something like:

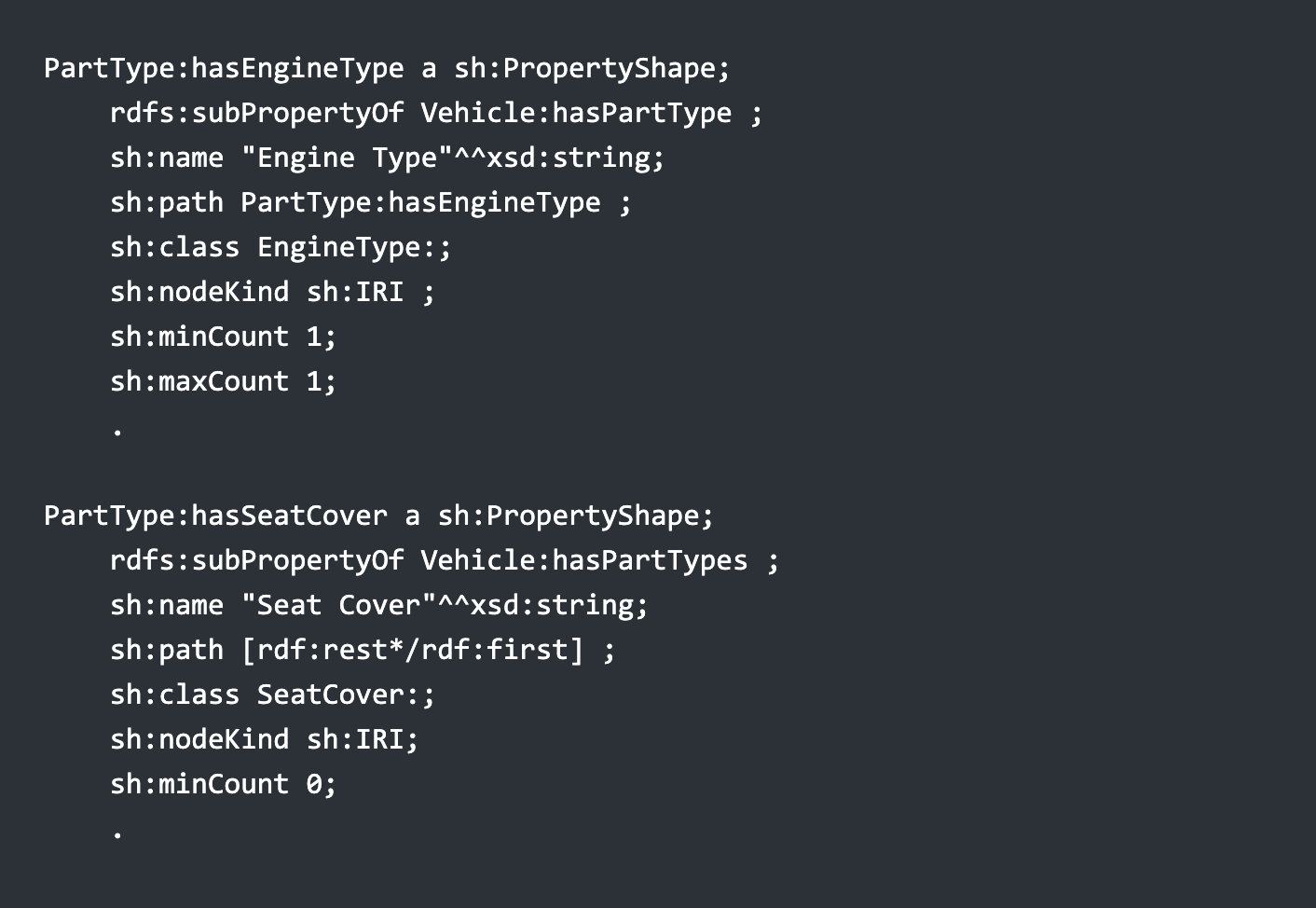
In this case, while the assumption in both cases is that the object type of the predicate is some form of PartType:, itself a subclass of Category: . The paths to get to that class are different. This suggests (correctly) that the generic (abstract) Vehicle:hasPartTypes property has neither path nor cardinality:

So what does this have to do with hypergraphs? Primarily hypergraphs are the association of data structures with relationships. Let’s take the bag approach as an example:

Named Graphs and Hypergraphs

Okay, you might be saying, “that makes sense for the object side of the equation, but what about the subject side?” (Of course, you may also be saying, "Gee, this article is too long; time for lunch”. It is Always hard to tell when you’re on this side of the blog.)

We use subject hypergraphs all the time. A graph is a set of assertions. You can refer to a set by name (the graph name), but what you’re actually talking about is the set of assertions:

This way, the part types are contained in a graph Graph:MyCar_PartTypes that uses the Category:isA property to identify the respective resources as being of the PartType: class.

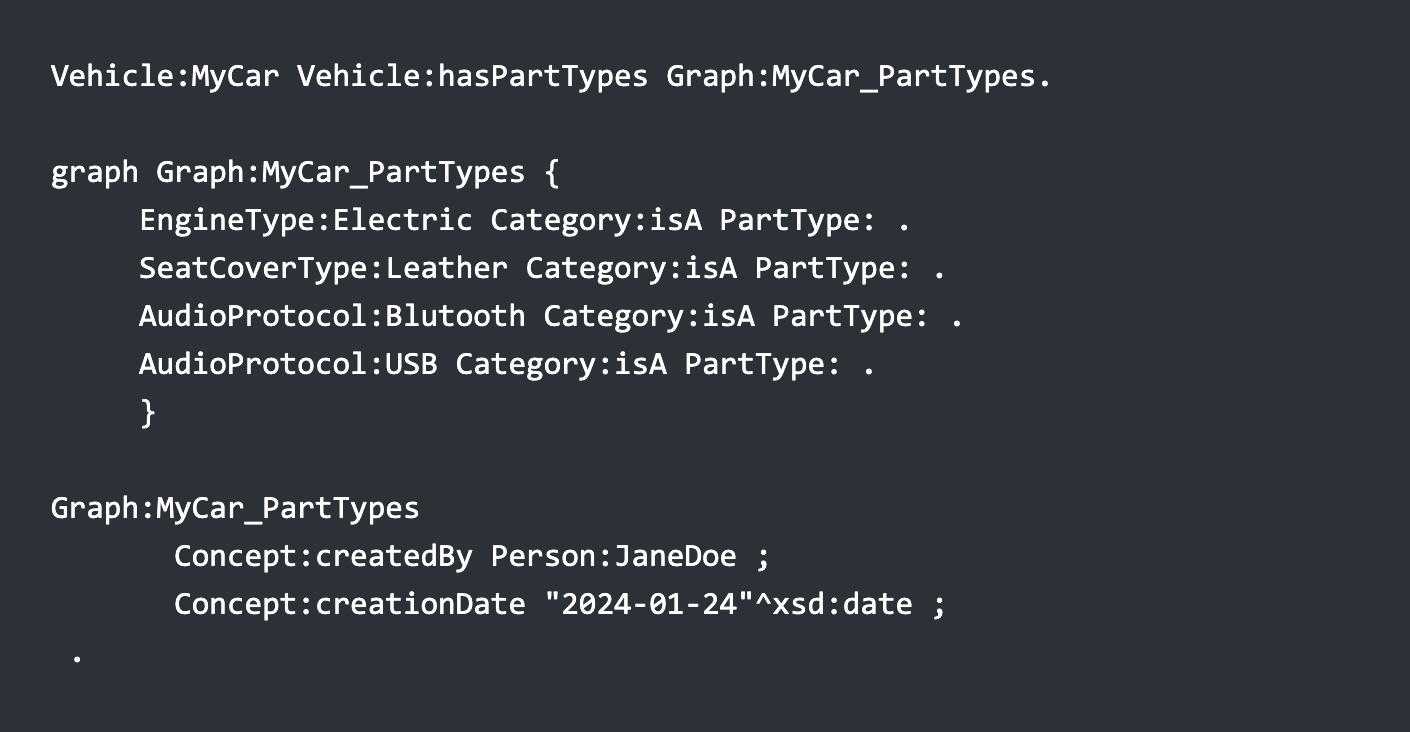
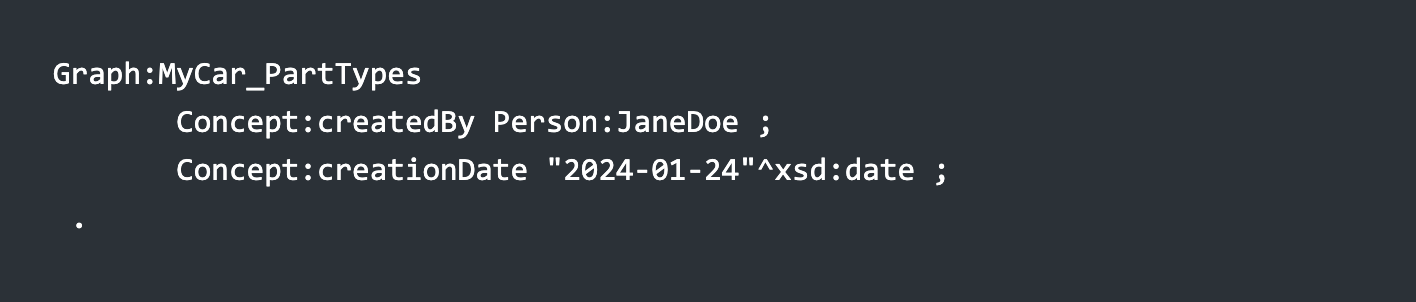
Here, Graph:MyCarPartTypes is a pointer to a set of triples. Note that this graph is referenced as both an object:

and as a subject:

The following indicates how you could then get the relevant part types from the graph in SPARQL, along with the author and creation date:

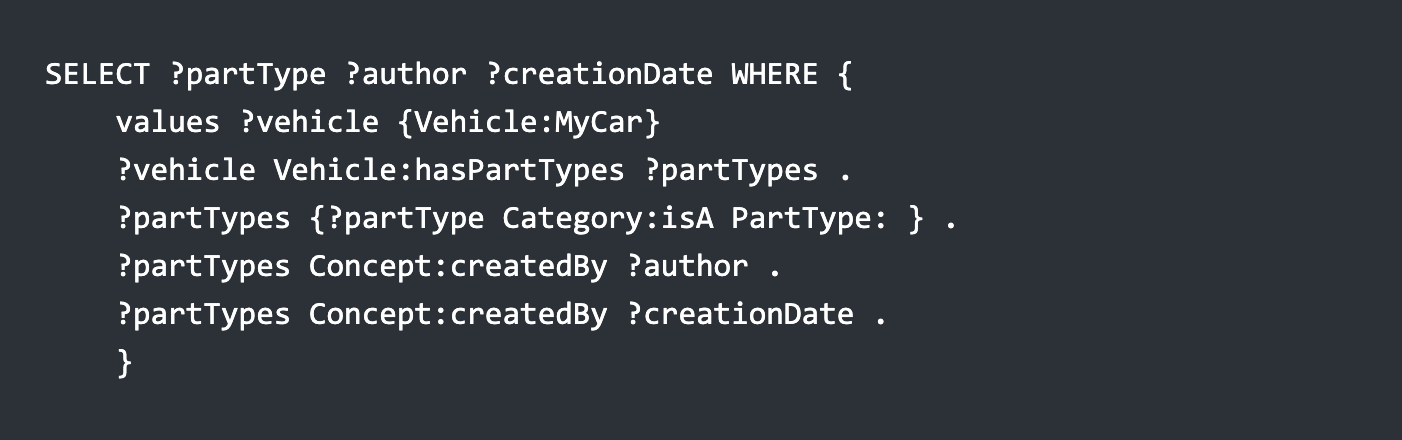
For the above data, this produces the table:

One additional point to consider. You may likely run into a situation where all possible categories and their definitions are kept in a graph called something like Graph:Categories . Thus, if the entry for EngineType:Electric includes a property called PartType:hasPTIN (Part Type InventoryNumber), like as follows:

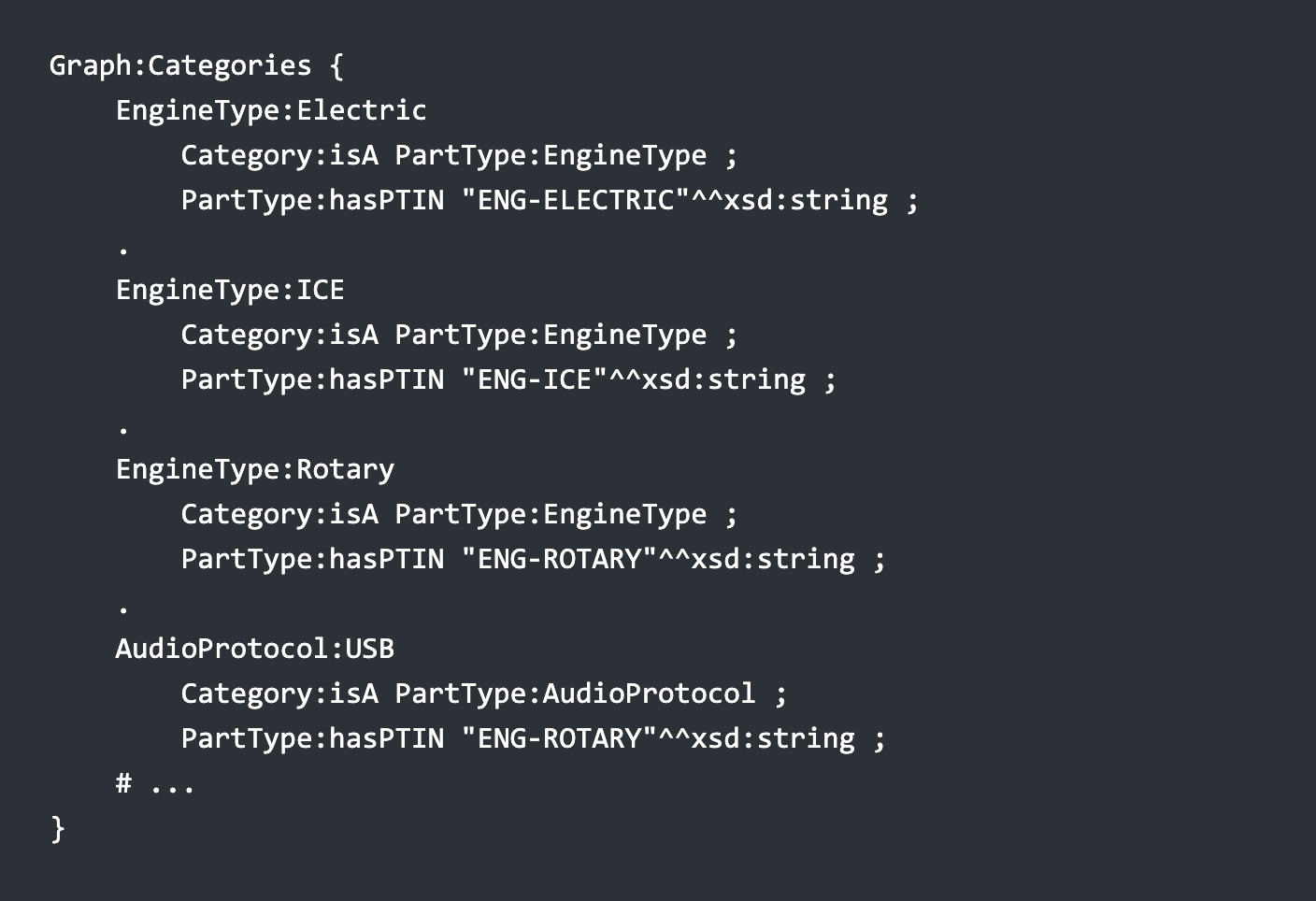
Then the SPARQL query to get the PTIN for that particular part type would look like the following:

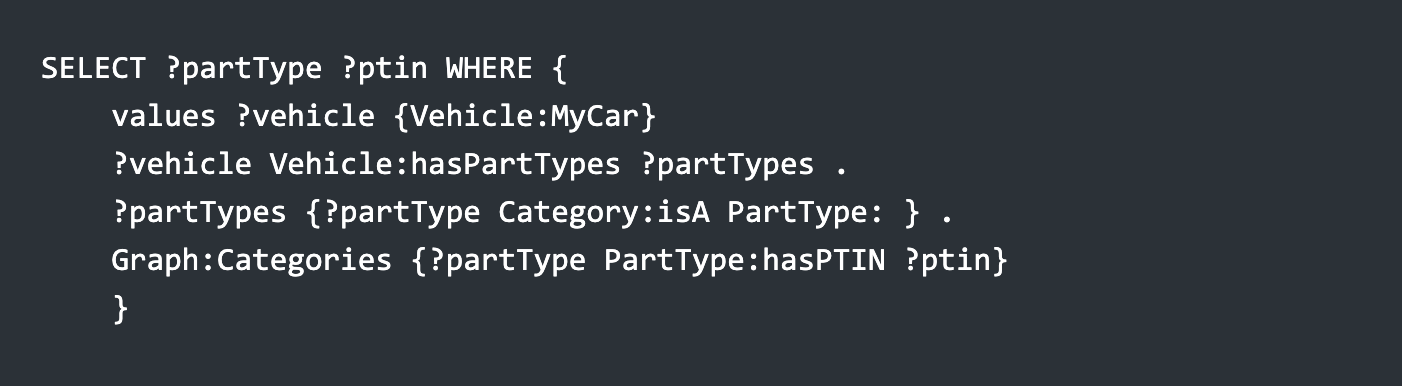
In other words, the graph Graph:MyCar_PartTypes holds the part types that the individual vehicle “MyCar” has as declarations, but the definition for those part types (and all of the others) is kept in Graph:Categories. This produces the table:

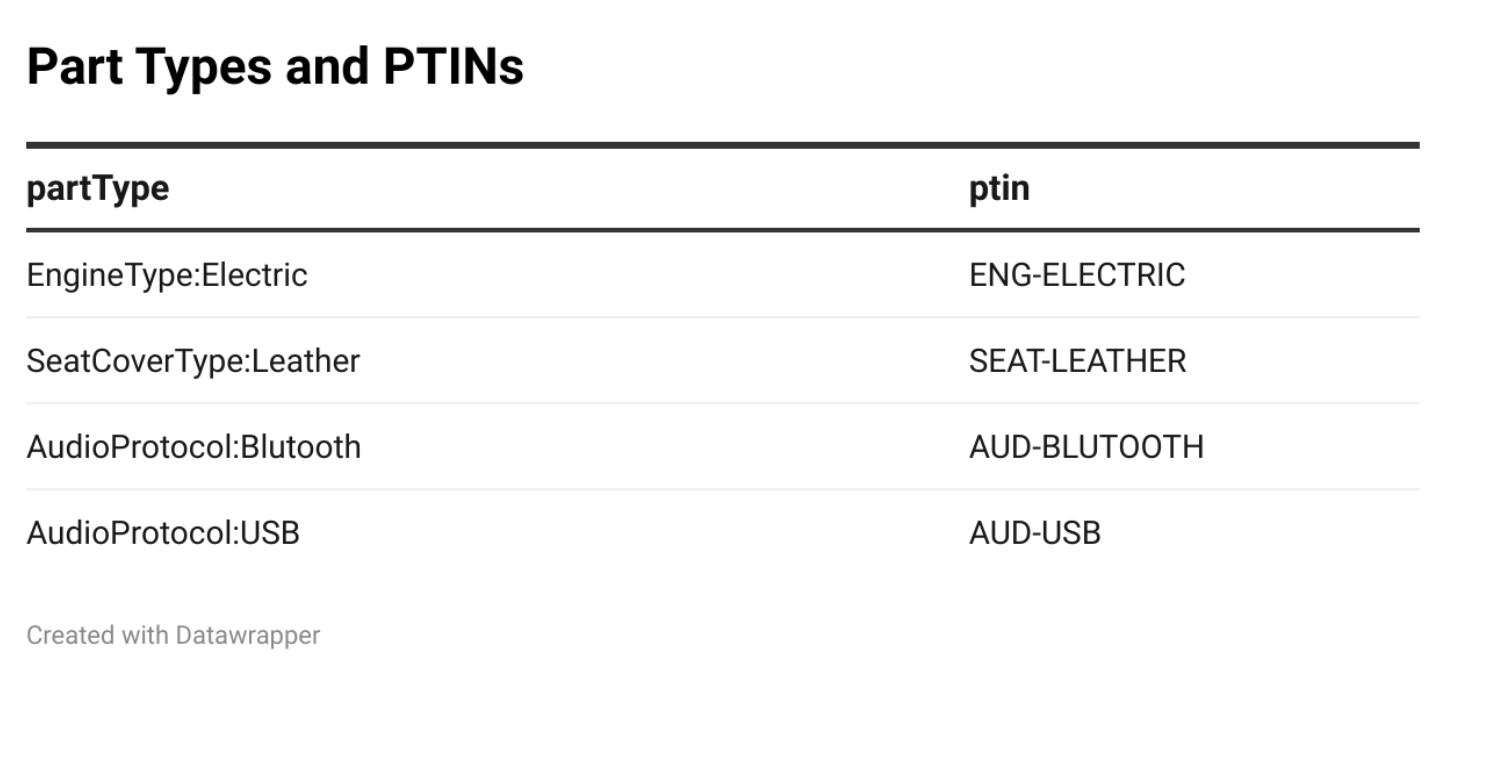
Turtle by itself does not have named graphs, however TRIG (Turtle RDF Graph Language) does. With the design patterns given above, TRIG crosses the threshold to being a hypergraph, because a graph is by definition a set (in this case a set of triples). What’s even more significant here is that while there is no easy way to identify an RDF List except via blank nodes (which are by definition not referenceable), named graphs are, perforce, named.

Getting Hyper

TRIG, Sparql 1.1 Query, and SPARQL 1.1 Update, which all hit the stage around the end of 2013, changed the nature of the game concerning named graphs, and hence, hypergraphs. Until then, everything within a triple store was effectively one giant graph. Even after these specs were published, it took a few years for named graphs to make their way into most triple stores, and many older ontologists were simply not trained on them and tended to ignore their implications. OWL, for instance, does not recognize named graphs as a formal concept, although there are OWL implementations that have been extended to do so.

SHACL code, the Shape Constraint Language encoded as triples, is typically stored in a named graph in the system, and one can pass the named graph URI as an argument to any processing code that needs to validate against that SHACL. Indeed, a typical SHACL validation process involves two graphs - the source graph that contains the nodes to be validated and the SHACL graphs that perform the validation.

Indeed, in theory, it should be possible to run a SPARQL UPDATE script that will identify, validate, and, if errors occur, generate reports on those nodes that do not satisfy the SPARQL constraints. In practice, that’s considerably more complicated to write such a script by hand. However, it should be possible to write an update script that, when given a SHACL graph, will generate a SPARQL update file that can, in turn, perform the requisite validation and reporting, including inline SPARQL.

Since SHACL also incorporates the ability to create constraint logic and define functions, this also means that SPARQL UPDATE and SHACL together, as hypergraphs, can generate self-modifying functional code. This is not the place to discuss the how of this, but it may be the subject of a subsequent post.

This is a form of generative hypergraph that can use graphs as objects, as endpoints for processes, and as tools for generating other content. As with most generative technologies, it may likely take advantage not only of tools like SPARQL and SPARQL UPDATE but also of AI-generated graphs and scripts, most likely instantiated through a SERVICE interface.

Additionally, SHACL can be used by reference to get relevant properties like OWL that don’t need complex pre-processing. This, too, is fodder for another post.

We’ve covered a lot of ground here. RDF Lists and bags provide a rudimentary hypergraph capability, though using named graphs expands that capability tremendously. This also does not consider perhaps the biggest aspect of hypergraphs - using a named graph or pointer to a structure as a predicate. That’s where things get very interesting indeed.

In media res,

Kurt Cagle