The Mathematics of Artificial Intelligence

Artificial Intelligence (AI) has revolutionized the way we live, work and interact with technology.

Its impact is felt in numerous areas of our lives, from personalized recommendations on streaming platforms to the development of autonomous vehicles. At the heart of AI lies mathematics, providing the foundation for the algorithms and models that make it possible. In this article, we will explore the mathematics behind AI and its role in advancing this rapidly evolving field.

Source: Medium

Linear Algebra

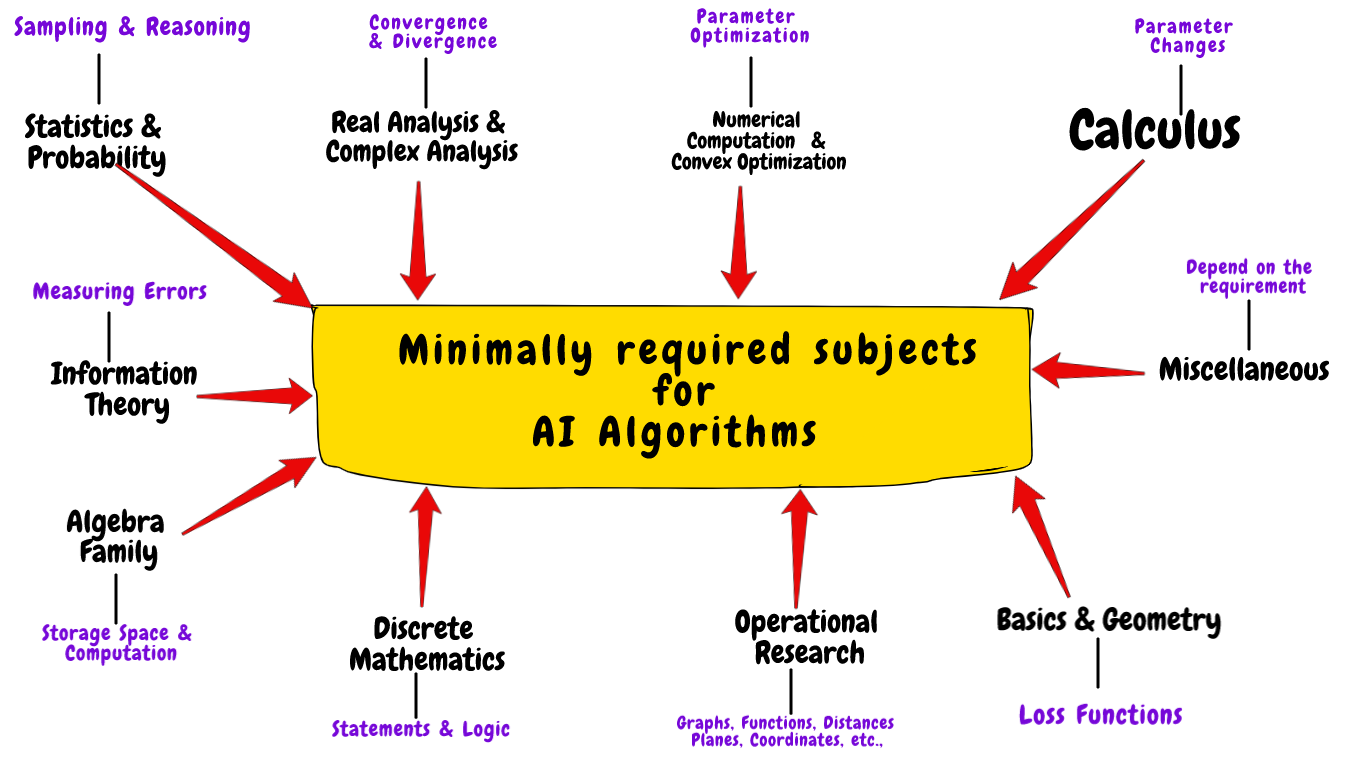
Linear algebra is a branch of mathematics that deals with linear systems and vector spaces. It is a fundamental tool for the representation and manipulation of data in AI.

As an example, in computer vision, linear algebra is used to represent and manipulate images and videos. In natural language processing, linear algebra is used to represent and manipulate text data. In both cases, linear algebra provides the foundation for the representation and manipulation of data, making it an essential component of AI.

Probability and Statistics

Probability and statistics provide the framework for making predictions and decisions based on data in AI. Probabilistic models, such as Bayesian networks, are used to model uncertainty and make predictions.

For instance, in autonomous driving, probabilistic models are used to make predictions about the likelihood of various outcomes, such as the likelihood of a pedestrian crossing a road, the likelihood of a traffic jam, and the likelihood of a road being blocked. These predictions are then used to make decisions about how to navigate the road.

Optimization

Optimization is a branch of mathematics concerned with finding the best solution to a problem. In AI, optimization algorithms are used to train models and find the best parameters for a given task.

Case in point, in machine learning, optimization algorithms are used to train models to perform a task, such as image classification or natural language processing. The goal of these algorithms is to find the best parameters for the model, such as the weights in a neural network, to minimize the error on the task.

Information Theory

Information theory provides the mathematical framework for understanding and measuring information in AI. It provides the tools for understanding the amount of information contained in a signal and for quantifying the amount of information that is lost or gained during a process.

In compression for example, information theory is used to measure the amount of information contained in a signal and to design algorithms that can compress the signal with minimal loss of information. In encryption, information theory is used to measure the amount of information that is protected by encryption algorithms and to design algorithms that can provide strong protection against attacks.

Conclusion

Mathematics plays a crucial role in the development of AI, providing the foundation for the algorithms and models that make it possible. From linear algebra and optimization to probability and statistics and information theory, the field of mathematics is essential to advancing the rapidly evolving field of AI.

As AI continues to evolve and impact our lives in new and exciting ways, the role of mathematics will continue to be critical, providing the foundation for the development of new algorithms and models that will drive the next generation of AI.